How Mathematics Shape Financial Decision-Making

Introduction :

The finance industry is an uncertain one. All insurance companies, investment firms, and central banks are asking themselves the same question: How can we determine the best course of action in such an unpredictable world? This is where mathematics comes in.

Mathematics is an exact science that has already proven itself in the world of finance. It is particularly perfect when it comes to identifying patterns or determining the probability of an event occurring or not. Of course, it is impossible for these mathematical models to predict the future exactly, but they are an excellent way for experts to find their bearings.

Today, the quantitative finance industry is booming. With the dazzling advances in Artificial Intelligence (AI), these firms have become indispensable to world leaders because their strategy is based on proven facts and precise mathematical formulas. Companies like Jane Street, Two Sigma, or Citadel dominate the markets with their increasingly sophisticated models and spare no expense to hire the brightest minds from around the world.

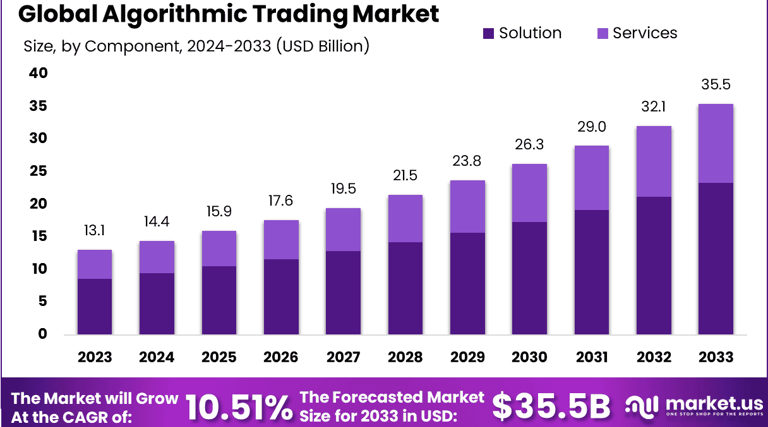
Quantifying uncertainty: Probabilities and Expected Value :

One of the fundamental roles of mathematics in finance is to transform uncertainty into numbers.

When we don't know what the future holds, we can still assign probabilities to each possible scenario and then calculate the expected value.

👉 Simple example:

An investor puts $100 into a stock.

50% chance of gaining $20

50% chance of losing $10

We calculate the expected value (E):

E=(0.5*20)+(0.5*-10)=10-5=5→ The average expected gain is $5, or an expected return of 5%.

But that's not all: variance and standard deviation measure how far the actual result can deviate from this average.

These measures of dispersion are used to assess risk.

👉 Real-world application:

Portfolio managers use these calculations to determine the trade-off between risk and return.

A stock may offer a high expected return, but also high variance → therefore more risky.

A bond offers a lower but more stable return → reduced risk.

This is what Harry Markowitz (1952) formalized in Modern Portfolio Theory, where the goal is to maximize the expected return for a given risk.

Optimization : Making the right Decision

Optimization is at the heart of financial mathematics: it involves finding the best solution among several possibilities according to specific criteria (minimizing risk, maximizing profit, etc.).

🔸 Example of portfolio optimization:

An investor wants to allocate their capital between two assets, A and B, in order to: achieve an expected return of 8% while minimizing risk (portfolio variance).

Mathematicians write this problem as an equation:

σₚ² = wₐ²σₐ² + wᵦ²σᵦ² + 2wₐwᵦCov(A,B)

wₐ,wᵦ: represents the weight of each asset in the portfolio. (E.g.: wa=40% means that it represents 40% of the portfolio and wb=60%)

σₐ,σᵦ: represents the variance of the variable, in other words the extent of the risk.

The total risk depends on:

• The specific risk of each asset,

• Their weight in the portfolio,

• And the correlation between them (the term 2wₐwᵦCov(A,B)).

Under constraint:

wₐ+wᵦ=1

E(Rp)=8%

In this example, we set a target expected return of 8%. In addition, we are told that all of the capital is invested.

This equation shows how the weights (the amounts invested in each asset) influence the overall risk.

Finance software solves this type of problem in a matter of milliseconds using convex optimization algorithms.

👉 Other examples of optimization:

• A bank chooses the best allocation of its funds between short- and long-term loans to maximize its return while complying with liquidity rules.

• A company seeks to set the optimal price for a product to maximize its profit based on expected demand.

Strategic Decision : Game theory

In finance, decisions are never isolated: each player (bank, investor, company) reacts to the choices of others.

This is where game theory, developed by John Nash and Von Neumann, comes in.

🔸 Classic example: the Prisoner's Dilemma

Two traders must decide whether to manipulate the market.

• If neither does → small gains for both.

• If only one cheats → he wins big, the other loses.

• If both cheat → the authorities intervene → losses for both.

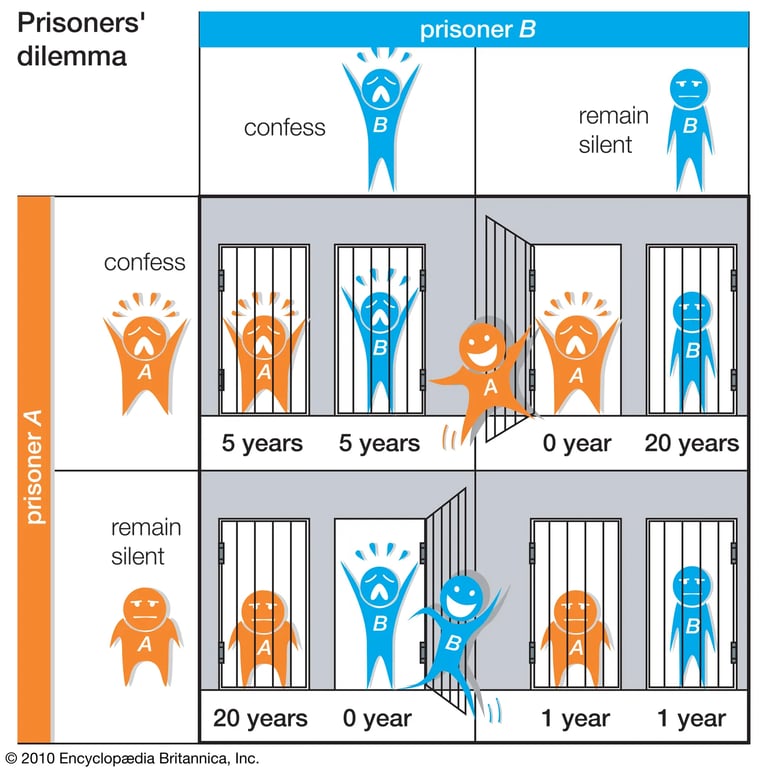
The Nash Equilibrium corresponds to a situation where no player has any interest in changing their strategy alone.

In finance, this helps to understand why:

• Companies adopt similar behaviors (pricing, investment strategy),

• Markets can remain “irrational” or speculative, as everyone anticipates the behavior of others.

👉 Other practical applications:

• Central banks and financial markets: the ECB or the Fed announce their policies while anticipating investor reactions.

• Mergers and acquisitions: two companies may choose between competition and cooperation depending on each other's strategies.

Game theory therefore provides a mathematical framework for financial strategy.

Limits of Mathematical Models :

Financial models are powerful, but they are based on assumptions.

When these assumptions no longer hold true, the model collapses.

👉 Real-life example: the 2008 financial crisis

Banks used models based on the normal distribution to estimate risks (Value at Risk, etc.).

These models assumed that extreme events were very rare.

But the crisis showed that “unlikely” events happen more often than we thought.

As Nassim Nicholas Taleb explained in The Black Swan, the problem was not the calculation, but the excessive confidence in the model.

👉 Another example:

A portfolio optimization model may assume that stock returns are independent—yet during a crisis, all markets fall together.

The result: diversification fails because correlations explode.

Thus, even though mathematics allows for rigorous risk analysis, it cannot replace human judgment or an economic understanding of the real world.